Abstract(摘要)
A purely peer-to-peer version of electronic cash would allow onlinepayments to be sent directly from one party to another without going through a financial institution. Digital signatures provide part of the solution, but the main benefits are lost if a trusted third party is still required to prevent double-spending. We propose a solution to the double-spending problem using a peer-to-peer network. The network timestamps transactions by hashing them into an ongoing chain of hash-based proof-of-work, forming a record that can not be changed without redoing the proof-of-work. The longest chain not only serves as proof of the sequence of events witnessed, but proof that it came from the largest pool of CPU power. As long as a majority of CPU power is controlled by nodes that are not cooperating to attack the network, they’ll generate the longest chain and outpace attackers. The network itself requires minimal structure. Messages are broadcast on a best effort basis, and nodes can leave and rejoin the network at will, accepting the longest proof-of-work chain as proof of what happened while they were gone.
本文提出了一种完全通过点对点技术实现的电子现金系统,它使得在线支付能够直接由一方发起并支付给另外一方,中间不需要通过任何的金融机构。虽然数字签名(Digital signatures)部分解决了这个问题,但是如果仍然需要第三方的支持才能防止双重支付(double-spending)的话,那么这种系统也就失去了存在的价值。我们在此提出一种解决方案,使现金系统在点对点的环境下运行,并防止双重支付问题。该网络通过随机散列(hashing)对全部交易加上时间戳(timestamps),将它们合并入一个不断延伸的基于随机散列的工作量证明(proof-of-work)的链条作为交易记录,除非重新完成全部的工作量证明,形成的交易记录将不可更改。最长的链条不仅将作为被观察到的事件序列(sequence)的证明,而且被看做是来自CPU计算能力最大的池(pool)。只要大多数的CPU计算能力都没有打算合作起来对全网进行攻击,那么诚实的节点将会生成最长的、超过攻击者的链条。这个系统本身需要的基础设施非常少。信息尽最大努力在全网传播即可,节点(nodes)可以随时离开和重新加入网络,并将最长的工作量证明链条作为在该节点离线期间发生的交易的证明。
Introduction(简介)
Commerce on the Internet has come to rely almost exclusively on financial institutions serving astrusted third parties to process electronic payments. While the system works well enough for most transactions, it still suffers from the inherent weaknesses of the trust based model. Completely non-reversible transactions are not really possible, since financial institutions can not avoid mediating disputes. The cost of mediation increases transaction costs, limiting the minimum practical transaction size and cutting off the possibility for small casual transactions,and there is a broader cost in the loss of ability to make non-reversible payments for non-reversible services. With the possibility of reversal, the need for trust spreads. Merchants must be wary of their customers, hassling them for more information than they would otherwise need.A certain percentage of fraud is accepted as unavoidable. These costs and payment uncertainties can be avoided in person by using physical currency, but no mechanism exists to make paymentsover a communications channel without a trusted party.What is needed is an electronic payment.
互联网上的贸易,几乎都需要借助金融机构作为可资信赖的第三方来处理电子支付信息。虽然在绝大多数情况下这类系统都运作良好,但是这类系统仍然内生性地受制于“基于信用的模式”(trust based model)的弱点。人们无法实现完全不可逆的交易,因为金融机构总是不可避免地会出面协调争端。而金融中介的存在,也会增加交易的成本,并且限制了实际可行的最小交易规模,也限制了日常的小额支付交易。并且潜在的损失还在于,很多商品和服务本身是无法退货的,如果缺乏不可逆的支付手段,互联网的贸易就大大受限。因为有潜在的退款的可能,就需要交易双方拥有信任。此外,因为商家也必须对自己的客户小心提防,所以会向客户索取完全不必要的个人信息。而实际的商业行为中,一定比例的欺诈性客户也被认为是不可避免的,相关损失视作销售费用处理。而在使用物理现金的情况下,因为此时没有第三方信用中介的存在,这些销售费用和支付问题上的不确定性却是可以避免的。
system based on cryptographic proof instead of trust,allowing any two willing parties to transact directly with each other without the need for a trusted third party. Transactions that are computationally impractical to reverse would protect sellers from fraud, and routine escrow mechanisms could easily be implemented to protect buyers. In this paper, we propose a solution to the double-spending problem using a peer-to-peer distributed timestamp server to generate computational proof of the chronological order of transactions. Thesystem is secure as long as honest nodes collectively control more CPU power than anycooperating group of attacker nodes
所以,我们非常需要这样一种电子支付系统,它基于密码学原理而不基于信用,使得任何达成一致的双方,能够直接进行支付,从而不需要第三方中介的参与。杜绝回滚(reverse)支付交易的可能,这就可以保护特定的卖家免于欺诈;而对于想要保护买家的人来说,在此环境下设立通常的第三方担保机制也可谓轻松加愉快。在这篇论文中,我们(we)将提出一种通过点对点分布式的时间戳服务器来生成依照时间前后排列并加以记录的电子交易证明,从而解决双重支付问题。只要诚实的节点所控制的计算能力的总和,大于有合作关系的(cooperating)攻击者的计算能力的总和,该系统就是安全的。
Transactions(交易)
We define an electronic coin as a chain of digital signatures. Each owner transfers the coin to the next by digitally signing a hash of the previous transaction and the public key of the next owner and adding these to the end of the coin. A payee can verify the signatures to verify the chain ofownership.
我们定义,一枚电子货币(an electronic coin)是这样的一串数字签名:每一位所有者通过对前一次交易和下一位拥有者的公钥(Public key) 签署一个随机散列的数字签名,并将这个签名附加在这枚电子货币的末尾,电子货币就发送给了下一位所有者。而收款人通过对签名进行检验,就能够验证该链条的所有者。
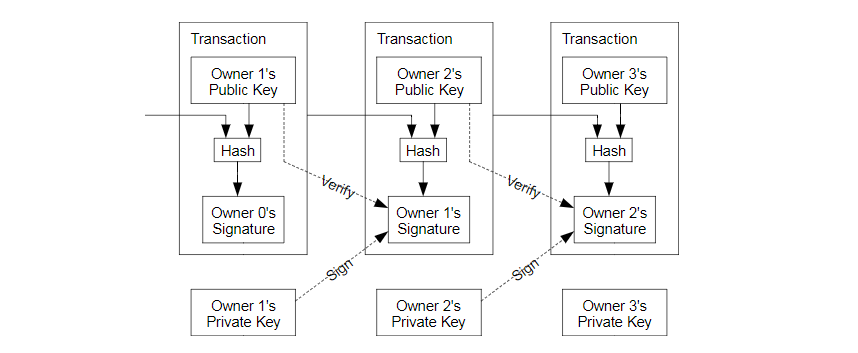
The problem of course is the payee can’t verify that one of the owners did not double-spend the coin. A common solution is to introduce a trusted central authority, or mint, that checks everytransaction for double spending. After each transaction, the coin must be returned to the mint to issue a new coin, and only coins issued directly from the mint are trusted not to be double-spent.The problem with this solution is that the fate of the entire money system depends on thecompany running the mint, with every transaction having to go through them, just like a bank.
该过程的问题在于,收款人将难以检验,之前的某位所有者,是否对这枚电子货币进行了双重支付。通常的解决方案,就是引入信得过的第三方权威,或者类似于造币厂(mint)的机构,来对每一笔交易进行检验,以防止双重支付。在每一笔交易结束后,这枚电子货币就要被造币厂回收,而造币厂将发行一枚新的电子货币;而只有造币厂直接发行的电子货币,才算作有效,这样就能够防止双重支付。可是该解决方案的问题在于,整个货币系统的命运完全依赖于运作造币厂的公司,因为每一笔交易都要经过该造币厂的确认,而该造币厂就好比是一家银行。
We need a way for the payee to know that the previous owners did not sign any earlier transactions. For our purposes, the earliest transaction is the one that counts, so we don’t care about later attempts to double-spend. The only way to confirm the absence of a transaction is to be aware of all transactions. In the mint based model, the mint was aware of all transactions and decided which arrived first. To accomplish this without a trusted party, transactions must be publicly announced [1], and we need a system for participants to agree on a single history of the order in which they were received. The payee needs proof that at the time of each transaction, the majority of nodes agreed it was the first received.
我们需要收款人有某种方法,能够确保之前的所有者没有对更早发生的交易实施签名。从逻辑上看,为了达到目的,实际上我们需要关注的只是于本交易之前发生的交易,而不需要关注这笔交易发生之后是否会有双重支付的尝试。为了确保某一次交易是不存在的,那么唯一的方法就是获悉之前发生过的所有交易。在造币厂模型里面,造币厂获悉所有的交易,并且决定了交易完成的先后顺序。如果想要在电子系统中排除第三方中介机构,那么交易信息就应当被公开宣布(publicly announced)1,我们需要整个系统内的所有参与者,都有唯一公认的历史交易序列。收款人需要确保在交易期间绝大多数的节点都认同该交易是首次出现。
Timestamp Server (时间戳服务器)
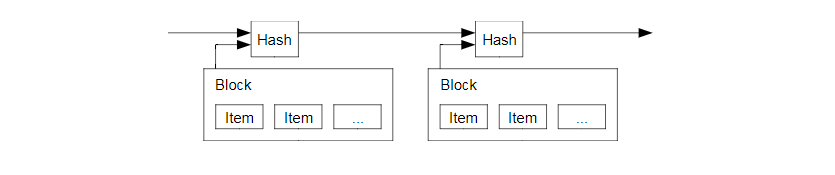
The solution we propose begins with a timestamp server. A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the hash, such as in a newspaper or Usenet post [2-5]. The timestamp proves that the data must have existed at the time, obviously, in order to get into the hash. Each timestamp includes the previous timestamp inits hash, forming a chain, with each additional timestamp reinforcing the ones before it.
本解决方案首先提出一个“时间戳服务器”。时间戳服务器通过对以区块(block)形式存在的一组数据实施随机散列而加上时间戳,并将该随机散列进行广播,就像在新闻或世界性新闻组网络(Usenet)的发帖一样[2-5]。显然,该时间戳能够证实特定数据必然于某特定时刻是的确存在的,因为只有在该时刻存在了才能获取相应的随机散列值。每个时间戳应当将前一个时间戳纳入其随机散列值中,每一个随后的时间戳都对之前的一个时间戳进行增强(reinforcing),这样就形成了一个链条(Chain)。
Proof-of-Work(工作量证明)
To implement a distributed timestamp server on a peer-to-peer basis, we will need to use a proof-of-work system similar to Adam Back’s Hashcash [6], rather than newspaper or Usenet posts. The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the hash begins with a number of zero bits. The average work required is exponential in the number of zero bits required and can be verified by executing a single hash.
为了在点对点的基础上构建一组分散化的时间戳服务器,仅仅像报纸或世界性新闻网络组一样工作是不够的,我们还需要一个类似于亚当·柏克(Adam Back)提出的哈希现金(Hashcash)[6]。在进行随机散列运算时,工作量证明机制引入了对某一个特定值的扫描工作,比方说SHA-256下,随机散列值以一个或多个0 开始。那么随着0 的数目的上升, 找到这个解所需要的工作量将呈指数增长,但是检验结果仅需要一次随机散列运算。
For our timestamp network, we implement the proof-of-work by incrementing a nonce in theblock until a value is found that gives the block’s hash the required zero bits. Once the CPU effort has been expended to make it satisfy the proof-of-work, the block can not be changed without redoing the work. As later blocks are chained after it, the work to change the block would include redoing all the blocks after it.
我们在区块中补增一个随机数(Nonce),这个随机数要使得该给定区块的随机散列值出现了所需的那么多个0。我们通过反复尝试来找到这个随机数,找到为止。这样我们就构建了一个工作量证明机制。只要该CPU 耗费的工作量能够满足该工作量证明机制,那么除非重新完成相当的工作量,该区块的信息就不可更改。由于之后的区块是链接在该区块之后的,所以想要更改该区块中的信息,就还需要重新完成之后所有区块的全部工作量

The proof-of-work also solves the problem of determining representation in majority decisionmaking. If the majority were based on one-IP-address-one-vote, it could be subverted by anyoneable to allocate many IPs. Proof-of-work is essentially one-CPU-one-vote. The majoritydecision is represented by the longest chain, which has the greatest proof-of-work effort invested in it. If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains. To modify a past block, an attacker would have to redo the proof-of-work of the block and all blocks after it and then catch up with and surpass thework of the honest nodes. We will show later that the probability of a slower attacker catching updiminishes exponentially as subsequent blocks are added.
同时,该工作量证明机制还解决了在集体投票表决时,谁是大多数的问题。如果决定大多数的方式是基于IP地址的,一IP地址一票,那么如果有人拥有分配大量IP地址的权力,则该机制就被破坏了。而工作量证明机制的本质则是一CPU一票。“大多数”的决定表达为最长的链,因为最长的链包含了最大的工作量。如果大多数的CPU为诚实的节点控制,那么诚实的链条将以最快的速度延长,并超越其他的竞争链条。如果想要对业已出现的区块进行修改,攻击者必须重新完成该区块的工作量外加该区块之后所有区块的工作量,并最终赶上和超越诚实节点的工作量。我们将在后文证明,设想一个较慢的攻击者试图赶上随后的区块,那么其成功概率将呈指数化递减。
To compensate for increasing hardware speed and varying interest in running nodes over time,the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour. If they’re generated too fast, the difficulty increases
另一个问题是,硬件的运算速度在高速增长,且节点参与网络的程度会有所起伏。为了解决这个问题,工作量证明的难度(the proof-of-work difficulty)将采用移动平均目标的方法来确定,即令难度指向令每小时生成区块的速度为某一预设的平均数。如果区块生成的速度过快,那么难度就会提高。
Network(网络)
The steps to run the network are as follows:
1)New transactions are broadcast to all nodes.
2)Each node collects new transactions into a block.
3)Each node works on finding a difficult proof-of-work for its block.
4)When a node finds a proof-of-work, it broadcasts the block to all nodes.
5)Nodes accept the block only if all transactions in it are valid and not already spent.
6)Nodes express their acceptance of the block by working on creating the next block in thechain, using the hash of the accepted block as the previous hash
运行该网络的步骤如下:
1) 新的交易向全网进行广播;
2) 每一个节点都将收到的交易信息纳入一个区块中;
3) 每个节点都尝试在自己的区块中找到一个具有足够难度的工作量证明;
4) 当一个节点找到了一个工作量证明,它就向全网进行广播;
5) 当且仅当包含在该区块中的所有交易都是有效的且之前未存在过的,其他节点才认同该区块的有效性;
6) 其他节点表示他们接受该区块,而表示接受的方法,则是在跟随该区块的末尾,制造新的区块以延长该链条,而将被接受区块的随机散列值视为先于新区快的随机散列值。
Nodes always consider the longest chain to be the correct one and will keep working onextending it. If two nodes broadcast different versions of the next block simultaneously, some nodes may receive one or the other first. In that case, they work on the first one they received,but save the other branch in case it becomes longer. The tie will be broken when the next proof-of-work is found and one branch becomes longer; the nodes that were working on the other branch will then switch to the longer one
节点始终都将最长的链条视为正确的链条,并持续工作和延长它。如果有两个节点同时广播不同版本的新区块,那么其他节点在接收到该区块的时间上将存在先后差别。当此情形,他们将在率先收到的区块基础上进行工作,但也会保留另外一个链条,以防后者变成最长的链条。该僵局(tie)的打破要等到下一个工作量证明被发现,而其中的一条链条被证实为是较长的一条,那么在另一条分支链条上工作的节点将转换阵营,开始在较长的链条上工作。
New transaction broadcasts do not necessarily need to reach all nodes. As long as they reach many nodes, they will get into a block before long. Block broadcasts are also tolerant of droppedmessages. If a node does not receive a block, it will request it when it receives the next block and realizes it missed one.
所谓“新的交易要广播”,实际上不需要抵达全部的节点。只要交易信息能够抵达足够多的节点,那么他们将很快被整合进一个区块中。而区块的广播对被丢弃的信息是具有容错能力的。如果一个节点没有收到某特定区块,那么该节点将会发现自己缺失了某个区块,也就可以提出自己下载该区块的请求。
Incentive(Conclusion)
By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. This adds an incentive for nodes to support the network, and providesa way to initially distribute coins into circulation, since there is no central authority to issue them.The steady addition of a constant of amount of new coins is analogous to gold miners expending resources to add gold to circulation. In our case, it is CPU time and electricity that is expended.
我们约定如此:每个区块的第一笔交易进行特殊化处理,该交易产生一枚由该区块创造者拥有的新的电子货币。这样就增加了节点支持该网络的激励,并在没有中央集权机构发行货币的情况下,提供了一种将电子货币分配到流通领域的一种方法。这种将一定数量新货币持续增添到货币系统中的方法,非常类似于耗费资源去挖掘金矿并将黄金注入到流通领域。此时,CPU的时间和电力消耗就是消耗的资源。
The incentive can also be funded with transaction fees. If the output value of a transaction is less than its input value, the difference is a transaction fee that is added to the incentive value of the block containing the transaction. Once a predetermined number of coins have entered circulation, the incentive can transition entirely to transaction fees and be completely inflation free
另外一个激励的来源则是交易费(transaction fees)。如果某笔交易的输出值小于输入值,那么差额就是交易费,该交易费将被增加到该区块的激励中。只要既定数量的电子货币已经进入流通,那么激励机制就可以逐渐转换为完全依靠交易费,那么本货币系统就能够免于通货膨胀。
he incentive may help encourage nodes to stay honest. If a greedy attacker is able toassemble more CPU power than all the honest nodes, he would have to choose between using itto defraud people by stealing back his payments, or using it to generate new coins. He ought tofind it more profitable to play by the rules, such rules that favour him with more new coins than everyone else combined, than to undermine the system and the validity of his own wealth.
激励系统也有助于鼓励节点保持诚实。如果有一个贪婪的攻击者能够调集比所有诚实节点加起来还要多的CPU计算力,那么他就面临一个选择:要么将其用于诚实工作产生新的电子货币,或者将其用于进行二次支付攻击。那么他就会发现,按照规则行事、诚实工作是更有利可图的。因为该等规则使得他能够拥有更多的电子货币,而不是破坏这个系统使得其自身财富的有效性受损。
Reclaiming Disk Space(回收磁盘空间)
Once the latest transaction in a coin is buried under enough blocks, the spent transactions before it can be discarded to save disk space. To facilitate this without breaking the block’s hash,transactions are hashed in a Merkle Tree [7][2][5], with only the root included in the block’s hash.Old blocks can then be compacted by stubbing off branches of the tree. The interior hashes donot need to be stored.
如果最近的交易已经被纳入了足够多的区块之中,那么就可以丢弃该交易之前的数据,以回收硬盘空间。为了同时确保不损害区块的随机散列值,交易信息被随机散列时,被构建成一种Merkle树(Merkle tree)[7]的形态,使得只有根(root)被纳入了区块的随机散列值。通过将该树(tree)的分支拔除(stubbing)的方法,老区块就能被压缩。而内部的随机散列值是不必保存的。
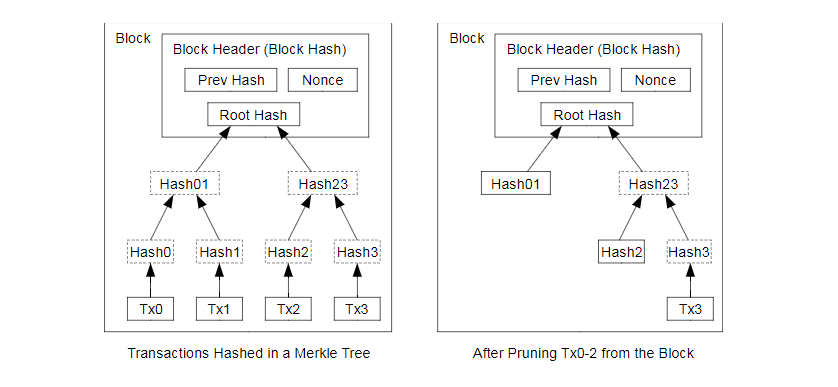
A block header with no transactions would be about 80 bytes. If we suppose blocks aregenerated every 10 minutes, 80 bytes 6 24 * 365 = 4.2MB per year. With computer systems typically selling with 2GB of RAM as of 2008, and Moore’s Law predicting current growth of1.2GB per year, storage should not be a problem even if the block headers must be kept inmemory.
不含交易信息的区块头(Block header)大小仅有80字节。如果我们设定区块生成的速率为每10分钟一个,那么每一年产生的数据位4.2MB。(80 bytes 6 24 * 365 = 4.2MB)。2008年,PC系统通常的内存容量为2GB,按照摩尔定律的预言,即使将全部的区块头存储于内存之中都不是问题。
Simplified Payment Verification(简化的支付确认)
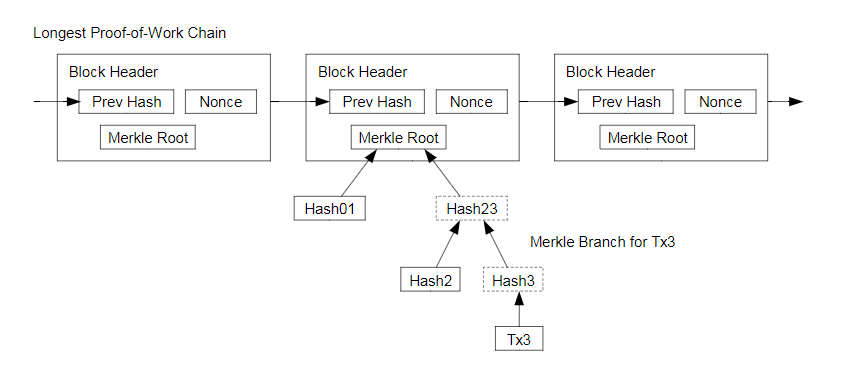
It is possible to verify payments without running a full network node. A user only needs to keep a copy of the block headers of the longest proof-of-work chain, which he can get by querying network nodes until he’s convinced he has the longest chain, and obtain the Merkle branch linking the transaction to the block it’s timestamped in. He can’t check the transaction for himself, but by linking it to a place in the chain, he can see that a network node has accepted it,and blocks added after it further confirm the network has accepted it.
在不运行完整网络节点的情况下,也能够对支付进行检验。一个用户需要保留最长的工作量证明链条的区块头的拷贝,它可以不断向网络发起询问,直到它确信自己拥有最长的链条,并能够通过merkle的分支通向它被加上时间戳并纳入区块的那次交易。节点想要自行检验该交易的有效性原本是不可能的,但通过追溯到链条的某个位置,它就能看到某个节点曾经接受过它,并且于其后追加的区块也进一步证明全网曾经接受了它。
As such, the verification is reliable as long as honest nodes control the network, but is more vulnerable if the network is over powered by an attacker. While network nodes can verify transactions for themselves, the simplified method can be fooled by an attacker’s fabricated transactions for as long as the attacker can continue to over power the network. One strategy to protect against this would be to accept alerts from network nodes when they detect an invalid block, prompting the user’s software to download the full block and alerted transactions to confirm the inconsistency. Businesses that receive frequent payments will probably still want to run their own nodes for more independent security and quicker verification.
当此情形,只要诚实的节点控制了网络,检验机制就是可靠的。但是,当全网被一个计算力占优的攻击者攻击时,将变得较为脆弱。因为网络节点能够自行确认交易的有效性,只要攻击者能够持续地保持计算力优势,简化的机制会被攻击者焊接的(fabricated)交易欺骗。那么一个可行的策略就是,只要他们发现了一个无效的区块,就立刻发出警报,收到警报的用户将立刻开始下载被警告有问题的区块或交易的完整信息,以便对信息的不一致进行判定。对于日常会发生大量收付的商业机构,可能仍会希望运行他们自己的完整节点,以保持较大的独立完全性和检验的快速性。
Combining and Splitting Value(价值的组合与分割)
Although it would be possible to handle coins individually, it would be unwieldy to make aseparate transaction for every cent in a transfer. To allow value to be split and combined,transactions contain multiple inputs and outputs. Normally there will be either a single inputfrom a larger previous transaction or multiple inputs combining smaller amounts, and at most two outputs: one for the payment, and one returning the change, if any, back to the sender.It should be noted that fan-out, where a transaction depends on several transactions, and those transactions depend on many more, is not a problem here. There is never the need to extract acomplete standalone copy of a transaction’s history.
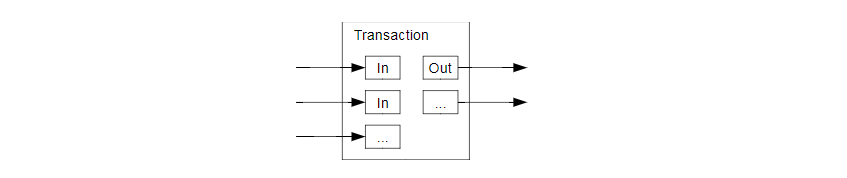
虽然可以单个单个地对电子货币进行处理,但是对于每一枚电子货币单独发起一次交易将是一种笨拙的办法。为了使得价值易于组合与分割,交易被设计为可以纳入多个输入和输出。一般而言是某次价值较大的前次交易构成的单一输入,或者由某几个价值较小的前次交易共同构成的并行输入,但是输出最多只有两个:一个用于支付,另一个用于找零(如有)。 需要指出的是,虽然一笔交易依赖于之前的多笔交易、这些交易又各自依赖于多笔交易,但是这并不存在任何问题。因为这个工作机制并不需要展开检验之前发生的所有交易历史。
Privacy(隐私)
The traditional banking model achieves a level of privacy by limiting access to information to the parties involved and the trusted third party. The necessity to announce all transactions publicly precludes this method, but privacy can still be maintained by breaking the flow of information in another place: by keeping public keys anonymous. The public can see that someone is sending an amount to someone else, but without information linking the transaction to anyone. This issimilar to the level of information released by stock exchanges, where the time and size ofindividual trades, the “tape”, is made public, but without telling who the parties were.
传统的造币厂模型为交易的参与者提供了一定程度的隐私保护,因为试图向可信任的第三方索取交易信息是严格受限的。但是如果将交易信息向全网进行广播,就意味着这样的方法失效了。但是隐私依然可以得到保护:将公钥保持为匿名。公众得知的信息仅仅是有某个人将一定数量的货币发所给了另外一个人,但是难以将该交易同某个特定的人联系在一起,也就是说,公众难以确信,这些人究竟是谁。这同股票交易所发布的信息是类似的,每一手股票买卖发生的时间、交易量是记录在案且可供查询的,但是交易双方的身份信息却不予透露。
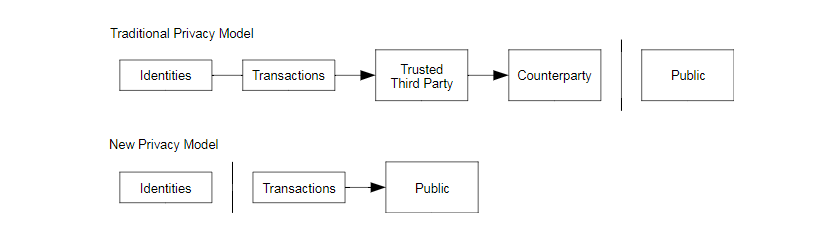
As an additional firewall, a new key pair should be used for each transaction to keep them from being linked to a common owner. Some linking is still unavoidable with multi-inputtransactions, which necessarily reveal that their inputs were owned by the same owner. The riskis that if the owner of a key is revealed, linking could reveal other transactions that belonged tothe same owner
作为额外的预防措施,使用者可以让每次交易都生成一个新的地址,以确保这些交易不被追溯到一个共同的所有者。不过由于存在并行输入,一定程度上的追溯还是不可避免的,因为并行输入暗示这些货币都属于同一个所有者。此时的风险在于,如果某个人的某一个公钥被确认属于他,那么就可以追溯出此人的其它很多交易。
Calculations(计算)
We consider the scenario of an attacker trying to generate an alternate chain faster than the honestchain. Even if this is accomplished, it does not throw the system open to arbitrary changes, such as creating value out of thin air or taking money that never belonged to the attacker. Nodes are not going to accept an invalid transaction as payment, and honest nodes will never accept a blockcontaining them. An attacker can only try to change one of his own transactions to take backmoney he recently spent.
设想如下场景:一个攻击者试图比诚实节点产生链条更快地制造替代性区块链。即便它达到了这一目的,但是整个系统也并非就此完全受制于攻击者的独断意志了,比方说凭空创造价值,或者掠夺本不属于攻击者的货币。这是因为节点将不会接受无效的交易,而诚实的节点永远不会接受一个包含了无效信息的区块。一个攻击者能做的,最多是更改他自己的交易信息,并试图拿回他刚刚付给别人的钱。
The race between the honest chain and an attacker chain can be characterized as a Binomial Random Walk. The success event is the honest chain being extended by one block, increasing its lead by +1, and the failure event is the attacker’s chain being extended by one block, reducing thegap by -1.
诚实链条和攻击者链条之间的竞赛,可以用二叉树随机漫步(Binomial Random Walk)来描述。成功事件定义为诚实链条延长了一个区块,使其领先性+1,而失败事件则是攻击者的链条被延长了一个区块,使得差距-1。
The probability of an attacker catching up from a given deficit is analogous to a Gambler’sRuin problem. Suppose a gambler with unlimited credit starts at a deficit and plays potentially aninfinite number of trials to try to reach breakeven. We can calculate the probability he everreaches breakeven, or that an attacker ever catches up with the honest chain, as follows [8]:
p = probability an honest node finds the next block
q = probability the attacker finds the next block
$q_z$ = probability the attacker will ever catch up from z blocks behind
攻击者成功填补某一既定差距的可能性,可以近似地看做赌徒破产问题(Gambler’s Ruin problem)。假定一个赌徒拥有无限的透支信用,然后开始进行潜在次数为无穷的赌博,试图填补上自己的亏空。那么我们可以计算他填补上亏空的概率,也就是该攻击者赶上诚实链条,如下所示[8]:
p=诚实节点制造出下一个节点的概率
q=攻击者制造出下一个节点的概率
qz=攻击者最终消弭了z个区块的落后差距
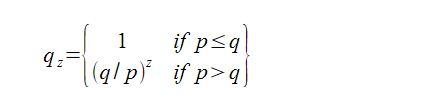
Given our assumption that p > q, the probability drops exponentially as the number of blocks theattacker has to catch up with increases. With the odds against him, if he doesn’t make a lucky lunge forward early on, his chances become vanishingly small as he falls further behind.We now consider how long the recipient of a new transaction needs to wait before being sufficiently certain the sender can’t change the transaction. We assume the sender is an attacker who wants to make the recipient believe he paid him for a while, then switch it to pay back to himself after some time has passed. The receiver will be alerted when that happens, but the sender hopes it will be too late.
假定p>q,那么攻击成功的概率就因为区块数的增长而呈现指数化下降。由于概率是攻击者的敌人,如果他不能幸运且快速地获得成功,那么他获得成功的机会随着时间的流逝就变得愈发渺茫。那么我们考虑一个收款人需要等待多长时间,才能足够确信付款人已经难以更改交易了。我们假设付款人是一个支付攻击者,希望让收款人在一段时间内相信他已经付过款了,然后立即将支付的款项重新支付给自己。虽然收款人届时会发现这一点,但为时已晚。
The receiver generates a new key pair and gives the public key to the sender shortly beforesigning. This prevents the sender from preparing a chain of blocks ahead of time by working onit continuously until he is lucky enough to get far enough ahead, then executing the transaction atthat moment. Once the transaction is sent, the dishonest sender starts working in secret on aparallel chain containing an alternate version of his transaction.
收款人生成了新的一对密钥组合,然后只预留一个较短的时间将公钥发送给付款人。这将可以防止以下情况:付款人预先准备好一个区块链然后持续地对此区块进行运算,直到运气让他的区块链超越了诚实链条,方才立即执行支付。当此情形,只要交易一旦发出,攻击者就开始秘密地准备一条包含了该交易替代版本的平行链条。
The recipient waits until the transaction has been added to a block and z blocks have beenlinked after it. He doesn’t know the exact amount of progress the attacker has made, butassuming the honest blocks took the average expected time per block, the attacker’s potentialprogress will be a Poisson distribution with expected value:
然后收款人将等待交易出现在首个区块中,然后在等到z个区块链接其后。此时,他仍然不能确切知道攻击者已经进展了多少个区块,但是假设诚实区块将耗费平均预期时间以产生一个区块,那么攻击者的潜在进展就是一个泊松分布,分布的期望值为:
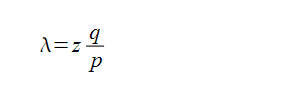
To get the probability the attacker could still catch up now, we multiply the Poisson density foreach amount of progress he could have made by the probability he could catch up from that point:
当此情形,为了计算攻击者追赶上的概率,我们将攻击者取得进展区块数量的泊松分布的概率密度,乘以在该数量下攻击者依然能够追赶上的概率。
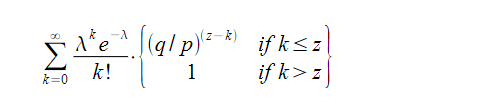
Rearranging to avoid summing the infinite tail of the distribution…
化为如下形式,避免对无限数列求和:
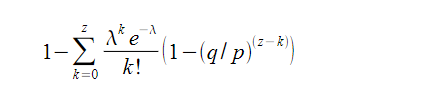
Converting to C code…
写为如下C语言代码:
Running some results, we can see the probability drop off exponentially with z.
对其进行运算,我们可以得到如下的概率结果,发现概率对z值呈指数下降。
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.000000
Solving for P less than 0.1%…
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
Conclusion(总结)
We have proposed a system for electronic transactions without relying on trust. We started with the usual framework of coins made from digital signatures, which provides strong control ofownership, but is incomplete without a way to prevent double-spending. To solve this, we proposed a peer-to-peer network using proof-of-work to record a public history of transactions that quickly becomes computationally impractical for an attacker to change if honest nodescontrol a majority of CPU power. The network is robust in its unstructured simplicity. Nodes work all at once with little coordination. They do not need to be identified, since messages are not routed to any particular place and only need to be delivered on a best effort basis. Nodes can leave and rejoin the network at will, accepting the proof-of-work chain as proof of what happened while they were gone. They vote with their CPU power, expressing their acceptance of valid blocks by working on extending them and rejecting invalid blocks by refusing to work onthem. Any needed rules and incentives can be enforced with this consensus mechanism.
我们在此提出了一种不需要信用中介的电子支付系统。我们首先讨论了通常的电子货币的电子签名原理,虽然这种系统为所有权提供了强有力的控制,但是不足以防止双重支付。为了解决这个问题,我们提出了一种采用工作量证明机制的点对点网络来记录交易的公开信息,只要诚实的节点能够控制绝大多数的CPU计算能力,就能使得攻击者事实上难以改变交易记录。该网络的强健之处在于它结构上的简洁性。节点之间的工作大部分是彼此独立的,只需要很少的协同。每个节点都不需要明确自己的身份,由于交易信息的流动路径并无任何要求,所以只需要尽其最大努力传播即可。节点可以随时离开网络,而想重新加入网络也非常容易,因为只需要补充接收离开期间的工作量证明链条即可。节点通过自己的CPU计算力进行投票,表决他们对有效区块的确认,他们不断延长有效的区块链来表达自己的确认,并拒绝在无效的区块之后延长区块以表示拒绝。本框架包含了一个P2P电子货币系统所需要的全部规则和激励措施
References(引用)
[1]W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998. 一种能够借助电子假名在群体内部相互支付并迫使个体遵守规则且不需要外界协助的电子现金机制
[2]H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimaltrust requirements,” In 20th Symposium on Information Theory in the Benelux, May 1999. 在最小化信任的基础上设计一种时间戳服务器
[3]S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In Journal of Cryptology, vol 3, no2, pages 99-111, 1991. 怎样为电子文件添加时间戳
[4]D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,”In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993. 提升电子时间戳的效率和可靠性
[5]S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In Proceedings of the 4th ACM Conferenceon Computer and Communications Security, pages 28-35, April 1997. 比特字串的安全命名
[6]A. Back, “Hashcash - a denial of service counter-measure,”http://www.hashcash.org/papers/hashcash.pdf, 2002 哈希现金——拒绝服务式攻击的克制方法
[7]R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980 Symposium on Security andPrivacy, IEEE Computer Society, pages 122-133, April 1980. 公钥密码体制协议
[8]W. Feller, “An introduction to probability theory and its applications,” 1957.9 概率论及其应用
声明
本文100%为组合翻译,详见引用,0%为原创
https:www.bitcoin.org/bitcoin.pdf
