【算法整理】A $*$ search 算法实现八数码问题

Posted on   |   In   |  

引言

最近帮一个朋友看八数码的问题，后来查了一下发现实际这是人工智能领域中的启发式搜索部分，网上给的答案看的都是一头雾水的，本文着重从降维映射的角度去实现一个简单的启发式搜索搜索算法。

图片名称

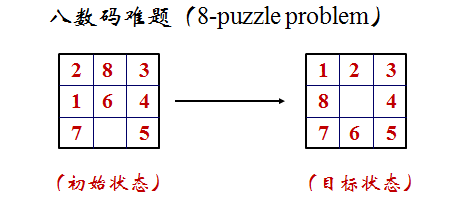
什么是八数码问题？

八数码问题也称为九宫问题。在3×3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。要求解决的问题是：给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。

所谓问题的一个状态就是棋子在棋盘上的一种摆法。棋子移动后，状态就会发生改变。解八数码问题实际上就是找出从初始状态到达目标状态所经过的一系列中间过渡状态。

八数码问题一般使用搜索法来解。搜索法有广度优先搜索法、深度优先搜索法、A算法等。这里通过用不同方法解八数码问题来比较一下不同搜索法的效果。

算法思路

我们的算法思路主要解决方案是将二维的数字进行降维，然后空格上下移动就体现在了数组下标的移动，然后对该一维数组进行“循环”，只到找到最符合条件的。
A. 如何表示空格节点状态？
在下面的算法中我们定义了将节点作为一个对象，这个对象有如下属性：当前8码数的状态、当前空白的位置、一共走了多少步、离我们的目标还有多少步、移动之前的状态。
B. 我们表示空格的上下移动？
我们将二维是数据（X，Y轴上的数据，上面的表格可以看成一个坐标）降为一位数组，空格的上下移动体现的是这个数组的下标移动
C. 如何有二维数组将为以为数组？
直接接在后面就好，例如：这里空格用状态0表示
2 8 3
1 6 4
7 0 5
转化成一维数组就是：283164705
D. 状态0的上下移动如何体现在一维数据的变化上？
状态0上移动，实际是状态0下标-3，状态0下移动，实际是状态0下标+3，
状态0左移动，实际是状态0下标-1，状态0右移动，实际是状态0下标+1，
E. 状态0如何不停“循环”？
状态0漫步目的移动。
F.何时停止？
符合某种状态条件的时候停止。

为每个棋牌制定一套可能的走步：左、上、右、下四种移动。这样就需32个操作算子。仅为空格制定这4种走步，因为只有紧靠空格的棋牌才能移动。空格移动的唯一约束是不能移出棋盘。结合上面我们说的降低维度，我们将算法实现结果如下

实现 A* search 算法

1.实现节点状态类

1
2
3
4
5
6
7
8
9
10
11
/**
 * 构造函数，8码数最初的状态
 * @param input An array representing a puzzle.
 */
public State(int[] input) {
  this.array = input;
  this.blankIndex = getIndex(input, 0);
  this.previous = null;
  this.g = 0;
  this.h = Puzzle.getHeuristic(this.array);
}

定义循环的终止条件，此部分可以根据实现方式最终的输出结果不同定义而不同，下面是输出常规型的八数码的终止条件

1
2
3
4
5
6
7
8
9
10
11
12
/**
 * 用来检查是否为解决，实际是一个循环终止条件
 * 这是正常的8数码
 * @return True if it is in the solved state, false if it is not.
 */
public boolean isSolved() {
  int[] p = this.array;
  for (int i = 1; i < p.length - 1; i++)
    if(p[i-1] > p[i]) return false;
  return (p[0] == 1);
}

2.定义实体Puzzle类

1
2
3
4
5
6
7
8
/**
   * Constructor for puzzle class.
   * @param puzzleInput Valid sliding puzzle in 2D array format.
   */
  public Puzzle(int[] puzzleInput) {
    this.initialState = new State(puzzleInput);
    this.state = this.initialState;
  }

Puzzle开始寻找（广度优先遍历），需要说明是下面启动了两个队列，一个已经访问过的队列，不算增加，还有一个是活动队列，进的同时也出。poll出来的数据主要用于判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * This method handles the solving of the puzzle.
 */
public void solve() {
  // Clear the queue and add the initial state.
  queue.clear();
  queue.add(this.initialState);
  long startTime = System.currentTimeMillis();
  int i = 0;
  while(!queue.isEmpty()) {
  	i++;
    // Get the best next state.
    this.state = queue.poll();
    // Check if the state is a solution.
    if (this.state.isSolved1()) {
  	  System.out.println(this.state.solutionMessage(startTime));
        return;
    }
    // Add this state to the visited HashSet so we don't revisit it.
    visited.add(state);
    // Add valid moves to the queue.
    this.addToQueue(Move.up(state));
    this.addToQueue(Move.down(state));
    this.addToQueue(Move.left(state));
    this.addToQueue(Move.right(state));
  }
}

3.定义移动类，主要解决二维数组移动时和一维数组的映射关系类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
 /**
  * 往上移动一下就是减去三
  * Returns a new state with the blank space swapped
  * with the tile above it.
  * @param state The state being operated on.
  * @return null if the state is invalid, the new state if valid.
  */
 public static State up(State state) {
//能往上移动的条件是目前不处于第一行
   if (state.blankIndex > 2)
     return new State(state, state.blankIndex - 3);
   return null;
 }
 /**
  * 往下移动一位就是加三
  * Returns a new state with the blank space swapped
  * with the tile below it.
  * @param state The state being operated on.
  * @return null if the state is invalid, the new state if valid.
  */
 public static State down(State state) {
//能往上移动的条件是目前不处于最后一行（第三行）
   if (state.blankIndex < 6){
   	return new State(state, state.blankIndex + 3);
   }
   return null;
 }
 /**
  * 
  * Returns a new state with the blank space swapped
  * with the tile to the left of it.
  * @param state The state being operated on.
  * @return null if the state is invalid, the new state if valid.
  */
 public static State left(State state) {
//能往左移动的条件是目前不处于第一列
   if (state.blankIndex % 3 > 0){
   	 return new State(state, state.blankIndex - 1);
   }
   return null;
 }
 /**
  * 能往右移动的条件是目前不处于最后一列(第三列)
  * 这里在队列中移动体现在队列+1
  * @param state The state being operated on.
  * @return null if the state is invalid, the new state if valid.
  */
 public static State right(State state) {
   if (state.blankIndex % 3 < 2){
   	 return new State(state, state.blankIndex + 1);
   }
   return null;
 }

4.写个测试类测试一下吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class PuzzleTest {
 
 public static void main(String[] args) {
	    Puzzle puzzle = null;
	    
	    if (args.length == 0){
	      puzzle = new Puzzle(Puzzle.getConsoleInput());
	    } 
	    // 检查是否可puzzle是否可解
	    /*if (!puzzle.isSolvable()) {
	       System.out.printf("Given puzzle:%s\n\nis NOT solvable!\n", puzzle.state.toString());
	       System.exit(0);
	    }*/
	    // Solve the puzzle.
	    puzzle.solve();
  }
}

输出结果：

Enter a valid 8-puzzle below:
2 8 3
1 6 4
7 0 5
Here are the steps to the goal state:

2 8 3
1 6 4
7 5

2 8 3
1 4
7 6 5

2 3
1 8 4
7 6 5

2 3
1 8 4
7 6 5

1 2 3
8 4
7 6 5

1 2 3
8 4
7 6 5

Given puzzle is SOLVED!
Solution took 2ms and 5 steps.

总结

上面只是简单的阐述了算法的实现思路，具体的算法代码可以从这里下载：点击这里


需要特别说明的是并不是所有的3×3的棋盘都能移动，因为需要在移动之前进行判断。

声明

本文30%为翻译组合,70%为原创

引用

http://www.cnblogs.com/guanghe/p/5485816.html
https://zhidao.baidu.com/question/195914427.html
https://github.com/caseyscarborough/puzzle

your support will encourage me to continue to create!
版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)