Diffie-Hellman密钥交换
Diffie-Hellman密钥交换是RSA之前的算法,其中的原理就是单项函数,如下图所示
在已知下图的模式下,任意跟换X可以获得不同的输出,但是从输出你无法获取X,RSA的算法基石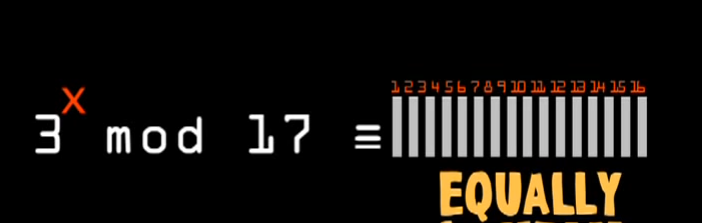
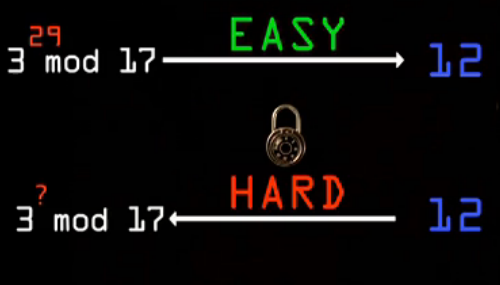
假设ALICE和BOB进行通信,而EVE是个监听者,首先ALICE根据上左边的选择一个任意的X54经过计算得出结果15发给BOB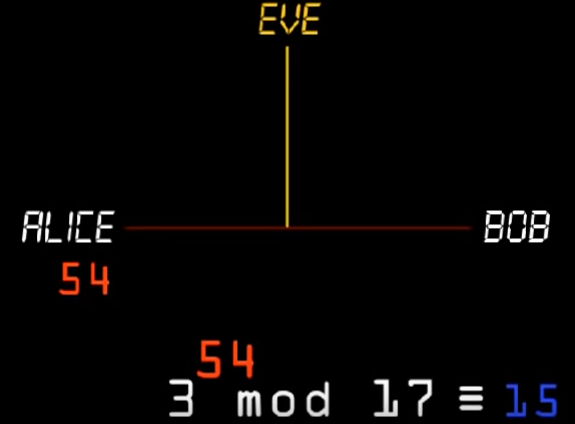
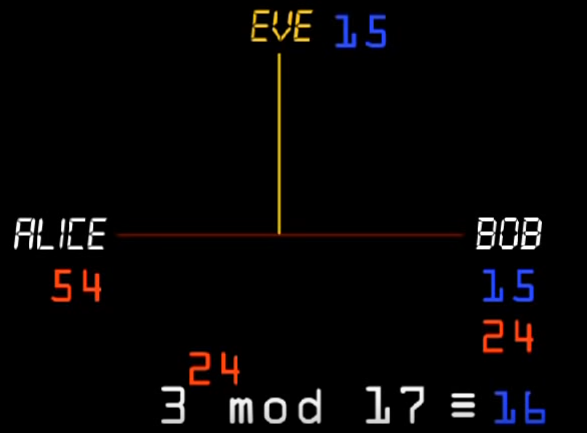
BOB同样选择任意一个X24按照上图的公式进行计算得出16,此时54,24分别为ALICE和BOB的私有,15和16则为公开的数据,监听者EVE可以获取15和16
其中1为将来需要交换的秘钥,两边接收的相同
$$3^{54\ast24}mod\quad17 =3^{24\ast54}mod\quad17 = 1$$
证明
$$16^{54}mod\quad17 = (3^{24}mod17)^{54}mod\quad17 = 3^{24\ast54}mod\quad17$$
同理
$$15^{24}mod\quad17 = (3^{54}mod17)^{24}mod\quad17 = 3^{54\ast24}mod\quad17$$
声明
本文70%为组合,详见引用,30%为原创
