【算法整理】曼哈顿距离

引言

最近帮一个朋友看八数码算法，在读源码的时候无意看到这个新奇的概念，后来发现其应用领域还挺广泛如游戏中的地图，特地研究了一下，本文的目的就是阐述下什么是曼哈顿距离以及其相近的概念，最后用算法实现在数组中如何计算两者之间的曼哈顿距离

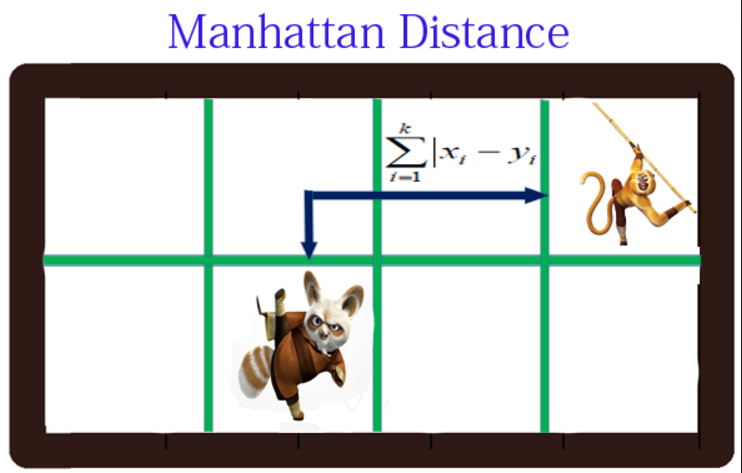
曼哈顿距离（出租车距离）

是由十九世纪的赫尔曼·闵可夫斯基所创词汇，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和
用以标明两个点在标准坐标系上的绝对轴距总和。下图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|xi-xj|+|yi-yj|。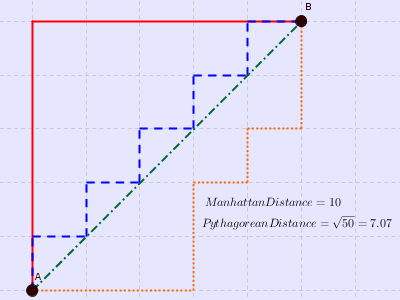

对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。

计算曼哈顿

3$*$3的矩阵，即如下所示
【A，B，C】
【D，E，F】
【G，H，I】
如何计算A和I之间的曼哈顿举例呢?

首先将其放入到数组【A，B，C，D，E，F，G，H，I】中，其他的详见注释

/**
* <p>Title: Test.java</p>
* <p>Description:一个计算曼哈顿距离的小程序 </p>
* <p>Copyright: Copyright (c) 2017</p>
* <p>Company: UOB</p>
* @author RuJia
* @date 2016年12月28日
* @version 1.0
* 【A，B，C】  
* 【D，E，F】    
* 【G，H，I】
*/
public class Test {
	public static void main(String[] args) {
		String i[] = {"A","B","C","D","E","F","G","H","I"};
		int s1 = getIndex(i,"A");
		int s2 = getIndex(i,"I");
		int m = getManhattanDistance(s1, s2);
		System.out.println("s1:"+s1+"----s2:"+s2+"-----m:"+m);
	}
		
	/**
	 * 根据当前的值返回在数组中的索引，这里的位置信息从1开始计算
	 * @param array
	 * @param value
	 * @return
	 */
	public static int getIndex(String[] array, String value) {
	    for (int i = 0; i < array.length; i++)
	      if (array[i].equals(value)) return i+1;
	    return -1;
	}
		
	/**
	 * 计算两点之间的曼哈顿,实际是在计算两者之间间隔的节点数
	 * @param satrt 起点
	 * @param end   终点
	 * @return
	 */
	public static int getManhattanDistance(int satrt, int end) {
		return Math.abs((satrt / 3) - ((end-1) / 3)) + Math.abs((satrt % 3) - ((end-1) % 3));
	}
}

输出结果：
s1:1—-s2:9—–m:3
刚好A和I之间隔了三个节点，他们是DGH或者DEF或者BEH

总结

本文简述了曼哈顿距离，并应用简单的代码实现了求解两点之间的哈夫曼举例。

声明

本文20%为翻译组合,80%为原创

引用

http://baike.baidu.com/link?url=gD-B1hbERwfSbqoz0r7ak6eu4Gu3eDVutRvuDRJxoNwT86NSWCVMoeiakF3y-jCDkGt5uTrhPthPXGxvL5BcHnuszx5sfYL2XsHunku1qqX4bwmtzr2EWZEu6tiXs3bf_3nEiMtuDaDhLHUYJUc5sK