引文
密码学是研究编制密码和破译密码的技术科学。研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。
在《一万字带您走进密码学的世界(上)》的文章中我们探讨了对称密码体系,哈希函数等技术,本文继续探讨密码学剩余的部分,本文的主要内容包括,非对称密码体系,签名算法等,因为本部分是区块链技术的基石,所以我会讲的更加详细一点,虽然我已经尽最大努力使思想简化,但是其中的数学理论对于很多人还是很晦涩,建议读者开始之前先读下数论的有关知识。本部分的主要结构如下:
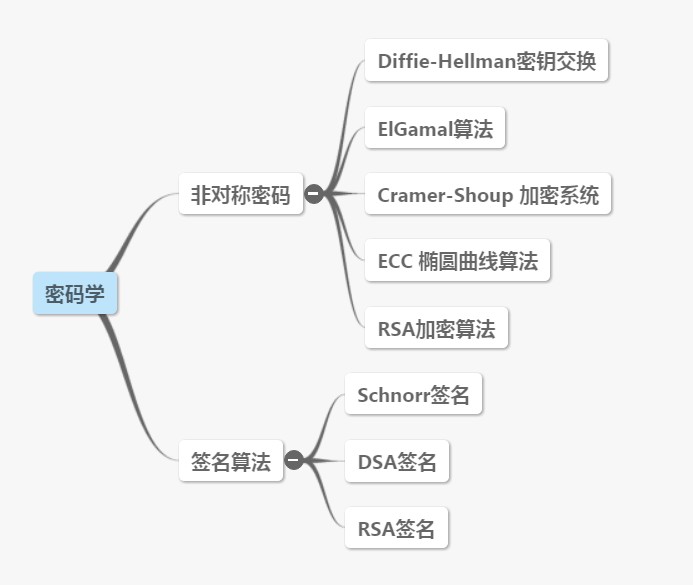
非对称密码
前面的文章我们探讨了对称加密,在对称秘钥加密的体系中,加密和解密使用同一个秘钥,显而易见的是这种方式存在一个很严重的弊端,那就是秘钥的分发和管理,一旦秘钥在分发过程中被人窃取,加密形同虚设。秘钥的管理也相当繁琐,如下图,如果我们要同时与n个人通信,那么每个人都将保存n-1个秘钥。

非对称的存在的意义就是为了克服这些问题,在非对称秘钥体系中,通信双方各有一个公钥和私钥,加密者使用私钥进行加密,然后传递解密者,解密者使用对方的公钥直接就可以解开,不存在秘钥秘钥传递的问题,为了更好的解释这个问题,下面用个简单的例子讲解一下。
一个简单的例子
Alice和Bob用传统信件进行沟通,假设Alice和Bob不相信有邮政系统,他们想在通信的时候把信件用箱子锁住,并且在箱子外面加上一个锁。
在公钥加密体系中,Alice首先将消息放在盒子中,然后锁上盒子用她的钥匙,然后将盒子发给bob,Bob收到盒子后然后用钥匙打开,很显然,这个钥匙一定是alice钥匙的副本,不然打不开

在上面的例子中我们知道,秘钥交换是一定存在的,在沟通之前一定要进行秘钥的交换,那么有没有其他的方案可以不进行秘钥交换呢,答案是有的,Alice首先将消息放在盒子中,然后锁上盒子用她的钥匙,然后将盒子发给bob,Bob收到盒子后然后用锁锁上,然后在返回给Alice,这个时候盒子上是有两把锁的,然后Alice去掉自己的锁,这样盒子上就剩下Bob的一把锁了,然后在将盒子发给Bob,Bob用自己的钥匙打开自己的锁,就看到其中的消息。

上面的方法是可以实现不用秘钥交换,但是确定就是过于复杂,那么有没有更好的方式呢?在对称密码体系中,问题将变得简单,Bob直接将自己的打开的锁发给Alice,Alice收到锁后,然后用这个锁加密锁住装有消息的盒子,然后发给Bob,Bob可以很轻易的打开自己的锁。

在这个方法中一个重要的环节就是在已知Bob的锁和箱子的时候时候,没有BOb的钥匙是一定是打不开,在显示生活中很容易理解,可以在计算机的世界中如何寻找到这样合适的算法,目前已知的算法有两种,一种是基于离散对数的问题,另一种是椭圆曲线连对数问题,在下面的算法中我们着重讲解离散对数的问题。
Diffie-Hellman密钥交换
Diffie-Hellman密钥交换首次出现在Diffie和Hellman的论文中,这篇影响深远的论文奠定了公开密钥密码编码学,因此该算法通常称之为Diffie-Hellman密钥交换。这种密钥交换技术的目的在于使得两个用户安全地交换一个秘密密钥以便用于以后的报文加密。
Diffie-Hellman加密算法的有效性依赖于计算离散对数的难度。简言之,可以如下定义离散对数:
首先定义一个素数p的原根,为其各次幂产生从1 到p-1的所有整数根,也就是说,如果a是素数p的一个原根,那么数值 $a mod p$,$a_1 mod p$,…,ap-1 mod p 是各不相同的整数,并且以某种排列方式组成了从1到p-1的所有整数。对于一个整数b和素数p的一个原根a,可以找到惟一的指数i,使得 b = ai mod p 其中0 ≤ i ≤ (p-1)指数i称为b的以a为基数的模p的离散对数或者指数,该值被记为inda,p(b)。
上面的一段引用看的一脸懵逼对吧,其实我也有又这样的感觉,我始终觉得一个优秀的学术工作者,要写出能读懂的文章,而不是别人看不懂的东西去彰显自己的高大上。好了就不吐槽了,我们开始用简单的例子解释上面的意思
首先说取摩运算,就是我们经常说的取余,比如我们对3对12进行取余就是3,9对12取余就是9,27对12取余就是3 简单点说:
$3^x mod 12= y $ 其中 $x \in (1,2,3…n)$ 在这里如果我们已知x,可以很轻易的计算出y的值,及时x的值比较大,利用计算机也可以很轻易的算出,但是如果已经y,即使用高性能的计算机也很难计算出x,这就是离散对数的问题。
离散对数公钥加密算法是目前最为热门的公钥加密算法 ,其安全性要远远高于基于大数分解的RSA算法,首先说明一下上述三位科学家公钥密码体制的运作过程(假定A和B两个人要在一个不安全通道如因特网上形成密钥以备日后加密解密所用)。
首先,A、B两人要共同公开约定一个素数q和有限域Fq中的一个生成元g;
A选定一个随机数a∈{1,2,…,q-1}(a可以认为是A之私钥),并将$g^a(mod \quad q)$传送给B;
B选定一个随机数b∈{1,2,…,q-1}(b可以认为是B之私钥),并将$g^b(mod \quad q)$传送给A;
此时A可以算出$(g^b)^a(mod \quad q)$,B也可以算出$(g^a)^b(mod \quad q)$,由于
$(g^b)^a(mod \quad q) = (g^a)^b(mod \quad q) = g^{ab}(mod \quad q)$,
因此,A和B就形成了一个公共的密钥$g^{ab}(mod \quad q)$,日后便可以此钥来进行传统的加密解密计算,从而达到在不安全的通道上进行保密通讯的目的。 显然,敌方可以截获到$g,q,g^a(mod \quad q),g^b(mod \quad q)$。因此,如果敌方有快速的求解离散对数的算法,就能从已截获的上述信息中迅速求出a或b,从而算出$g^ab(mod \quad q)$。遗憾的是,目前世界上根本就没有快速的求解离散对数的算法,因此当所选的有限域Fq很大时,a或b就很难算出。
Diffie-Hellman的算法举例可以参考我之前的文章《【密码学】Diffie-Hellman密钥交换》
ElGamal算法
在密码学中,ElGamal加密系统是一个基于迪菲-赫尔曼密钥交换的非对称加密算法。它在1985年由塔希尔·盖莫尔提出。GnuPG和PGP等很多密码学系统中都应用到了ElGamal算法。
ElGamal加密算法可以定义在任何循环群$ {\displaystyle G}$ 上。它的安全性取决于 ${\displaystyle G}$ 上的离散对数难题。
ElGamal 加密被用于免费的GNU隐私保护软件、PGP 近期的版本和其他密码系统中

此部分的详细讲解,请看下篇文章《【密码学】ElGamal算法详解》
Cramer-Shoup 加密系统
Cramer–Shoup 系统是一个非对称秘钥加密算法,而且被证实是第一个针对适应性选择米文攻击所采用的标准加密猜想所用的安全有效的项目。其安全性是基于决定性Diffie–Hellman猜想的计算难解性(广泛接受,但未被证实)的计算难解性的。由 Ronald Cramer (罗纳德·克莱默)和 Victor Shoup (维克多·苏伯)于1998年研发,是 ElGamal 加密系统的延伸。与 ElGamal 相反,它具有很强的延展性,Cramer–Shoup 添加了另外的成分来确保甚至是遭受广泛的攻击时保证其非延展性。这一非延展性是通过使用抗撞击哈希函数和额外的计算而取得的,导致了密文是 ElGamal 的两倍大
ECC 椭圆曲线算法
椭圆曲线密码学(英语:Elliptic curve cryptography,缩写为ECC),一种建立公开金钥加密的算法,基于椭圆曲线数学。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。
ECC的主要优势是在某些情况下它比其他的方法使用更小的密钥——比如RSA加密算法——提供相当的或更高等级的安全。ECC的另一个优势是可以定义群之间的双线性映射,基于Weil对或是Tate对;双线性映射已经在密码学中发现了大量的应用,例如基于身份的加密。不过一个缺点是加密和解密操作的实现比其他机制花费的时间长。
RSA加密算法
RSA加密算法是一种非对称加密算法。在公开密钥加密和电子商业中RSA被广泛使用。RSA是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的。

因为此部分是区块链的算法结合比较紧密,我将花更多的篇幅讲解,从上面的讲解我们知道,我们需要构建一个锁和一把钥匙,然后将锁分配给每个人,然后自己保留钥匙,在这里这把锁就相当于相当于公钥,自己的钥匙就相当于私钥,下面我们开始用离散对数问题来构建我们的公钥和私钥。虽然在部分我会尽量写的详细,但是在开始之前,读者最好能对数论知识有个基本的了解,可以参数我之前的文章《【密码学】RSA算法解析-数论基础》
我们前面已经提到离散对数的问题,形如
$$m^e mod \quad N = c$$
我们在已知c和N和m的情况下很难图导出e.同样的道理,你在已知c和N和e,的情况下也很难推出来m,这就是一个典型的单项函数

m是明文,c是密文,e是加密的钥匙,d是解密的钥匙,按照我们上面的解释,在下面的加密解密过程都是严谨的单向过程
$$m^e mod \quad N = c \quad\quad公式1$$
我们找到一个d使下面的公式也成立
$$c^d mod \quad N = m \quad\quad公式2$$
1.接下来我们的目标就是找到合适的e和d,我们开始推导,将公式1带入到公式2中
$$(m^e mod \quad N)^d mod \quad N = m \quad\quad公式3$$
$$(m^e)^d mod \quad N = m \quad\quad公式4$$
$$ m^{ed} mod \quad N = m \quad\quad公式5$$
2.我们将一个数n的子集存在互质关系个数定义为φ(n),那么一个合数的公约数是不固定的,但是一个素数的公约数一定只有自己,所以对于素数φ(n) = n-1 这个求解过程叫欧拉函数,可以参考我之前的文章
3.欧拉函数主要应用在欧拉定理上,”欧拉定理”指的是:如果两个正整数m和N互质,则n的欧拉函数 φ(n) 可以让下面的等式成立:
$$m^{\phi({n})}\equiv 1(mod\quad N) \quad\quad公式6$$
转换后就是:
$$m^{\phi({n})} mod\quad N \equiv 1 \quad\quad公式7 $$
然后两边同时乘以m
$$m^{\phi({n})+1} mod\quad N \equiv m \quad\quad公式8$$
有上面的公式5我们知道
$$ m^{ed} mod \quad N = m \quad\quad公式5$$
因此可以得出
$$ m^{ed} mod \quad N = m^{\phi({n})+1} mod\quad N $$
$$ed = \phi({n})+1$$
$$ed - \phi({n}) y = 1 \quad\quad\quad此处增加y表示任意数字$$
我们目前已经知道的条件,我们已知N,一般N都是两个素数的乘积,已经知道加密秘钥e,求解解密秘钥d
为了便于讲解,我们假设在这里N=77,则$phi({n})=6*10 = 60$, e等于67,则计算过程如下,
$$67d - 60 y = 1$$
以为y可以为负数,因此
这是有一个二项式的接,其实有多个答案,我们只需获取其中一个就可以,根据欧几里得拓展定理可以算出私钥d的值为43,计算机过程参考《【密码学】RSA算法解析-加密解密》
最终加密过程
$$75^{67}\equiv c(mod\quad 77)$$
在计算机中可以很轻易的计算出c=26
解密过程
$$26^{43}\equiv m(mod\quad 77)$$
在计算机中可以很轻易的计算出m=75
演示代码

python源码地址:
https://cloud.sagemath.com/projects/dc18d6fb-c4ae-47c4-8ea4-b2a1887ccb6b/files/RSA_CASE.sagews
到这里RSA完整的讲完了,虽然我已经写得很详细了,但是肯定还是有些读者不能完全理解,如果还是不能理解,建议先学习点数论的知识预热。
签名算法
我们在讨论签名算法之前,先来回忆一下之前讲的hash函数,我们有一份文件可以计算出他的Hash值,一旦文件被篡改做产生的Hash值也将变化,Hash函数解决了完整性的问题,然而并没有解决认证的问题,如果攻击者不但把文件给篡改了还把hash值给改了,这样接收者就察觉不到文件已经出了问题。
我们需要一种签名机制,这种签名机制能保证所有人都能对文件的完整性进行认证,同时又能验证这份文件确实是发送者发的,攻击者无法伪造这个签名。
设计原则
数字签名常常和哈希函数在一起使用,给定一段明文M,我们可以计算出明文的哈希值h(M),然后将哈希值进行某种加密S后,附在明文上,结构如下:
$$M|S(h(M))$$
在上述结构主要依赖于哈希值不存在对撞,即不同的明文之间不会存在相同的哈希值,实际上每种公钥加密体系都能实现,下面我们主要探究3种: Schnorr签名,Digital Signature Algorithm(数字证书签名),RSA签名
Schnorr签名
Schnorr签名是基于ElGamal算法的,它的安全性取决于离散对数的难题。
DSA签名
使用SHA哈希加密函数,它的安全性也取决于离散对数的难题。它是1990被提出,并且已经被US FIPS所接受,他的具体原理如下:
1.选择一个1024位的素数p,此时有一个群组$Z_p$
2.选择另一个160位的素数q,q除以p-1和q都在群组$G_q$中,并且群组$G_q$属于$Z_p$
3.其中要到的哈希算法是SHA-1
秘钥生成:
1.选择p和q,条件就是上面所表达的,换成数学的表达方式就是$p=zq+1$ 并且z属于群组$Z_p$
2.选择一个g,使下面的公式成立,$ jz = g(mod \quad p) $ 并且 $1<j<p$
3.在范围${1,…..q-1}$ 的选择一个随机数x
4.计算出来$y=g^x mod \quad p$
5.其中公钥就是$K^1 = (p,q,g,y)$,私钥就是$K^2 = (p,q,g,x)$
签名过程:
1.在范围${1,…..q-1}$的选择一个随机数r
2.计算出来$s=(g^r mod \quad p ) mod \quad q $
3.计算出$t=((SHA-1(M)+xs)r^{-1}) mod \quad q$
4.将签名结果$(s,t)$附属在消息上。
验签过程:
1.计算出$u_1 = (SHA-1(M)t^{-1}) mod \quad q $
2.计算出$u_2 =(s*t^{-1}) mod \quad q$
3.计算签名$s^1 = ((g^{u_1}y^{u_2})mod \quad p) mod \quad q$
4.比较$s^1$是否与s相同
RSA签名
一种从RSA算法演变而来的签名,它的安全性取决大素数分解难题。下面我们来看看具体的实现过程
秘钥生成
1.选择两个大素数,p和q
2.计算出他们的欧拉函数,$\phi(n) = (p-1)(q-1) $
3.我们选择一个整数e>1,并使$gcd(e,\phi(n))=1$ 即e要和欧拉函数(非公约的个数),互为素数。
4.我们使$de = 1( mod \phi(n)) $ ,根据欧几里得拓展定理计算出d.
5.然后我们就得到了公钥$K1= (e,n)$,然后对外发布公钥
6.私钥就是$k2=d$
签名过程:
我们假设需要加密的信息为M,其中M在${1,,,,n-1}$这个范围内,h为哈希加密函数,则签名的过程如下:
$$s=h(M)^d mod \quad n$$
验签过程:
计算出明文的哈希值h(M)比较h(M)是否和$s^e\quad n$相应,如果相同则验签成功。
总结
本文主要阐述了密码学中的非对称密码和签名算法,不得不说对于一个开发人员来说,今天的讲解过的理论化,但是理论是实践的基础,不是吗?
声明
本文45%为翻译组合,55%为原创
引用
http://www.jiamisoft.com/blog/index.php/3165-diffie-hellmanjiamisuanfa.html
https://zh.wikipedia.org/wiki/RSA%E5%8A%A0%E5%AF%86%E6%BC%94%E7%AE%97%E6%B3%95
http://baike.baidu.com/link?url=14BKIalgIoeD2Wbq7X6rxUBoYrTEHlhxlX3x337N7_7qLaDh6XMK1MMStd5zIfROme-meST7ZJPQqWDjb7MgUJHxPiVeEJqeP2PB1i2eSNOZAzy_c-BgpCQLLUjn1GHg
https://www.khanacademy.org/computing/computer-science/cryptography/modern-crypt/v/checkpoint-advanced-lessons http://en.wikipedia.org/wiki/Cramer–Shoup_cryptosystem
https://zh.wikipedia.org/wiki/%E6%A4%AD%E5%9C%86%E6%9B%B2%E7%BA%BF%E5%AF%86%E7%A0%81%E5%AD%A6
