引言
为了给区块链研究做铺垫,我们今天研究的是验证报文完整性的方法:密码学的函数函数,当然有些文章也将哈希函数称为散列函数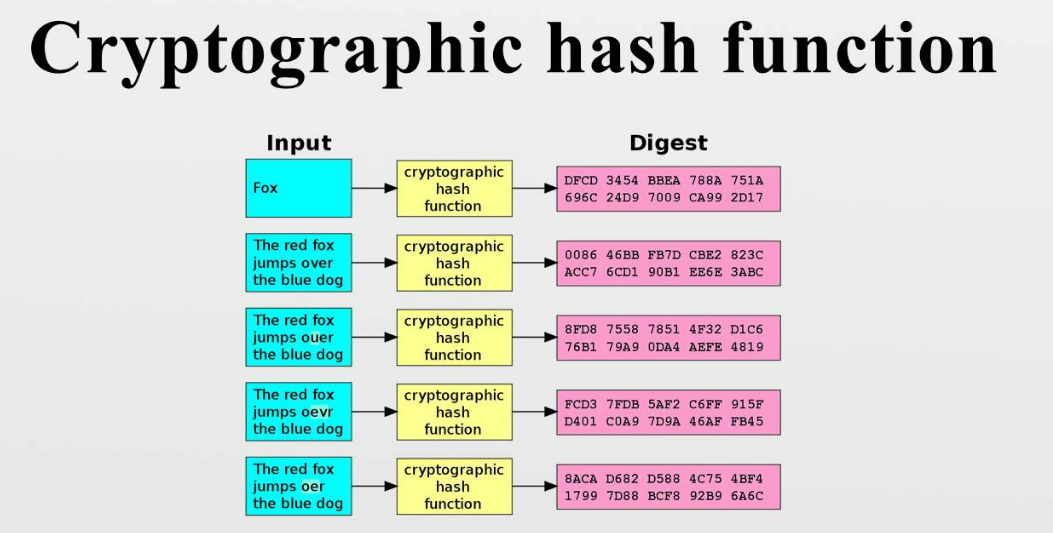
密码学哈希函数
密码学上的哈希函数是一种测试消息完整性的方法,哈希函数可以输入任意长的信息,然后输出一个固定长度的字符串,这个字符串就叫做hash值,散列函数原则上用于以下方式:
假设爱丽丝想要给鲍勃一些方法使鲍勃能确认完整的接收了她发来的信息,她可以将信息的摘要伴随着的信息(可能已经加密)一起发给鲍勃,一旦鲍勃接收到了信息,鲍勃就可以用相同的方法再次算出这段信息的摘要,然后将新的摘要和爱丽丝发来的进行对比。如果相同则说明消息是完整的,如果不同,那么鲍勃就知道这些数据可能在传输途中遭到黑客篡改。况且爱丽丝不希望黑客能推算出发送的消息哪些是摘要,一旦黑客能区分出哪些部分是摘要,就能伪造报文和对应的摘要,当然这不适合我们今天探讨的话题,言归正传,密码学上指散列函数应该具有哪些特征。
- 输入长度可以是任意长度
- 输出是固定长度
- 给出任意的报文可以很轻松的算出哈希函数$H(x)$
- 哈希函数是个不可逆的函数,就是给出一个$Y $,其中$Y = H(x)$,你完全不能通过Y去推算出x
- 哈希函数不存在碰撞,就是不存在任意一个$x’$,使$H(x’) = H(x)$
密码学哈希函数和编程中的哈希函数
我在写这篇文章的时候一直在哈希函数前面强调是密码学上的哈希函数,只是因为它与编程中的哈希函数不同,编程上的哈希函数(表)是一种数据结构,哈希表是将数据对象映射到一个便于存储和检索的特定内存空间。虽然和密码学上的哈希函数有点类似,都是一段长的数据映射到固定长度的短的值,但是哈希表是可逆的,相同的数据可以允许多个不用的哈希编码实现方式去做地址映射,而密码学上的哈希函数则是透明的不可逆的。
SHA-256
关于哈希函数的算法有很多种,比如MD4,MD5,SHA1(这些已经不安全了)等,因为我们在这里探讨的是为了区块链做准备的,所以我们直接进入主题。
SHA (Secure Hash Algorithm,译作安全散列算法) 是美国国家安全局 (NSA) 设计,美国国家标准与技术研究院 (NIST) 发布的一系列密码散列函数。正式名称为 SHA 的家族第一个成员发布于 1993年。然而现在的人们给它取了一个非正式的名称 SHA-0 以避免与它的后继者混淆。两年之后, SHA-1,第一个 SHA 的后继者发布了。 另外还有四种变体,曾经发布以提升输出的范围和变更一些细微设计: SHA-224, SHA-256, SHA-384 和 SHA-512。
SHA-2的第t个加密循环。图中的深蓝色方块是事先定义好的非线性函数。ABCDEFGH一开始分别是八个初始值,Kt是第t个密钥,Wt是本区块产生第t个word。原消息被切成固定长度的区块,对每一个区块,产生n个word(n视算法而定),通过重复运作循环n次对ABCDEFGH这八个工作区块循环加密。最后一次循环所产生的八段字符串合起来即是此区块对应到的散列字符串。若原消息包含数个区块,则最后还要将这些区块产生的散列字符串加以混合才能产生最后的散列字符串。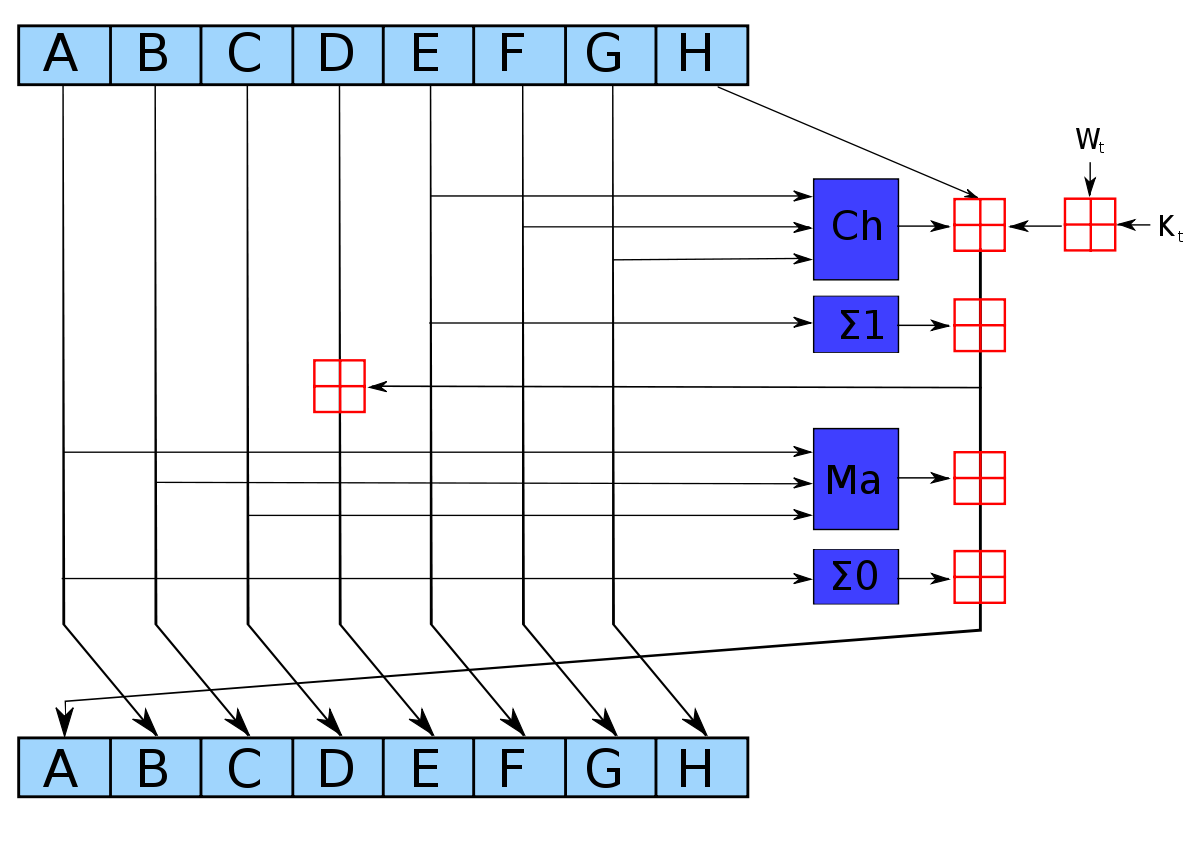
网络教程上有各种语言的关于SHA-256的实现库,这里就不重复了
各种哈希函数的对比
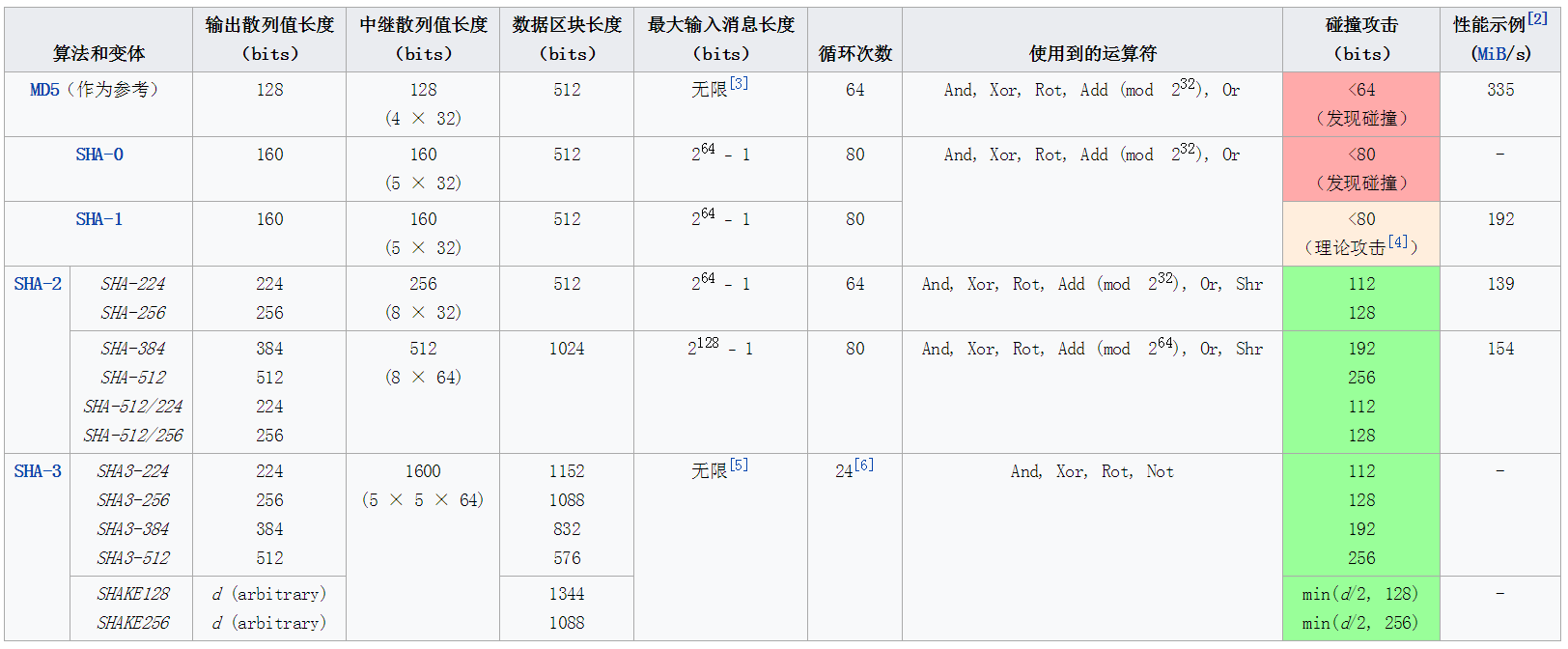
总结
本文是为区块链研究做背景的内容,主要浅谈了密码学上的哈希函数,以及此哈希函数与编程上的哈希函数的区别,最后探讨了SHA-256
声明
本文50%为组合,50%为原创
