引言
上次文章中提到椭圆曲线加密算法,因为此部分过于学术就没有详细讲解,最近有读者问及,索性写篇文章整理下此算法,首先椭圆曲线加密算法是用于比特币中的公钥私钥的生成。需要指出的是在非对称密钥体系中,椭圆曲线加密算法只是其中的一种,可能还有其他的算法,比如Elgamal,DSA等。今天的主要内容包括:群(GROUP)组的概念,椭圆曲线加密算法与相关的类比与例子
单向陷门函数
A trapdoor function is a function that is easy to compute in one direction, yet difficult to compute in the opposite direction (finding its inverse) without special information, called the “trapdoor”. Trapdoor functions are widely used in cryptography. –wikipedia
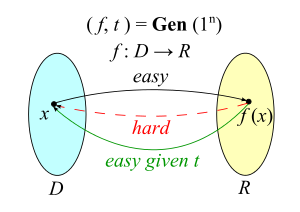
一个trapdoor函数最大的功能就是单向计算非常容易,在缺少必要信息的情况下逆向计算非常困难,这就是公私钥密码使用的基础:用私钥推出公钥很容易,有公钥反推出私钥却很困难,除非具备了某些必要的参数。非对称密钥的发展史就是一个在不停的寻找优秀单项函数的过程,目前常用有DH,DSA,ECDH,ECDSA.我们今天探讨的椭圆曲线加密算法(ECDSA),只是其中的一种。下面开始探讨椭圆曲线加密算法为何是一个优秀的Trapdoor函数。
一个有趣的类比
一个椭圆曲线是满足一个特殊方程的点集。一个椭圆曲线方程看起来有点像这个:$y^2 = x^3 + ax + b$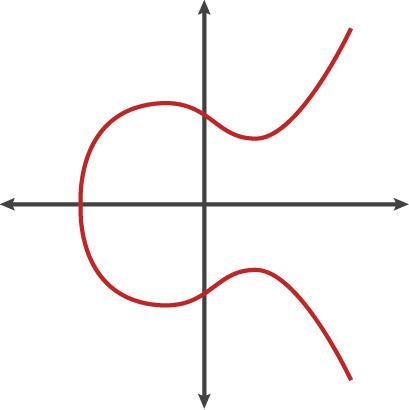
也有其他椭圆曲线的代表,但学术上一个椭圆曲线是一个满足一个变量为二阶,另一个变量为3阶的二元方程。一个椭圆曲线不仅仅是一个漂亮的图片,它也有一些使它成为密码学的一个好环境的性能。
靠近看上文标绘的椭圆曲线。它有几个有趣的特性。
其中一个是水平对称。曲线上的任何点以X轴反射并且仍然是同样的曲线。一个更加有趣的特性是任何不垂直的线穿过曲线最多有三个交点。让我们来把曲线想象成一个奇异的桌球游戏。取曲线上的任意两点并且把他们连起来;这条线与曲线有两个以上的交点。在这个桌球游戏里,你拿球从A射向B.当它撞上曲线,这个球向上反弹(它位于X轴以下)或者向下反弹到曲线的另一边。
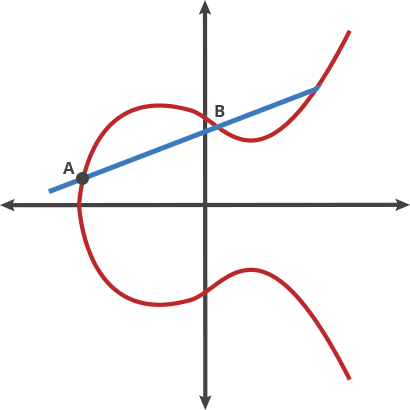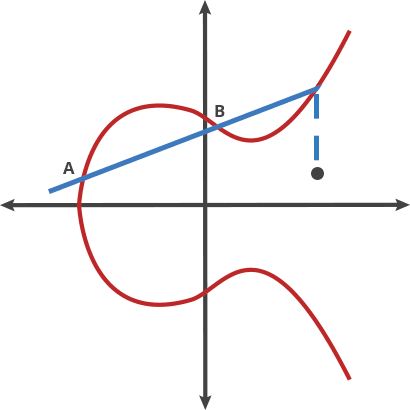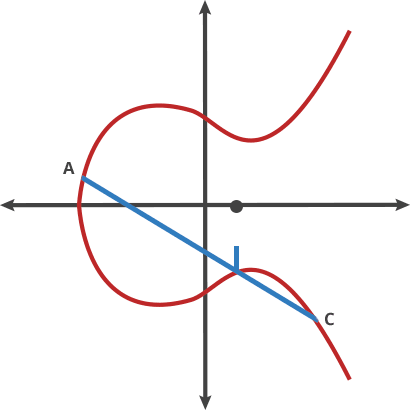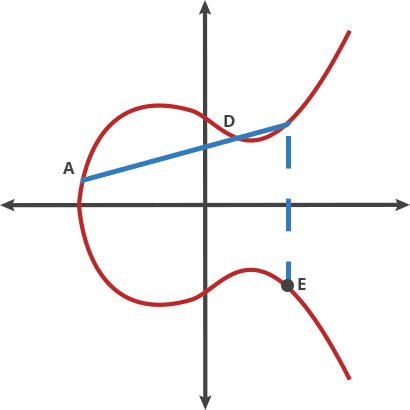
我们把球移向两点叫“打点(dot)”。曲线上的任意两点能被同时打点得到一个新点。
A dot B = C
我们也能同时做一串移动来用它自己反复“打点”。
A dot A = B
A dot B = C
A dot C = D
…
事实证明如果你有两个点,一个最初的点用它自己打点n次到达一个最终点,在你只知道最重点时找到n和最初点是很难的。继续我们的奇异桌球比喻,想象一个人在一段任意时间里在一个房间里单独玩我们游戏。对他来说,他跟着上述规则来反复击球是容易的。如果一个人后来走进房间并且看到球最终的位置,即使他们知道这个游戏的所有规则和球的起点,在没有全程观察游戏直到球到达同一点的情况下,他们也不能算出球击打到那的次数。容易做,但很难解开。这就是一个非常棒的trapdoor函数的基础。
椭圆曲线
按照上面的例子,如果我们需要桌球进行反弹来确定不同的点,那么桌面一定是具有一定范围的,不然发射出去永远接触不到面永远找不到反射点了,在数学中我们把这个桌面成为定义成一个群,为了便于讲解我们将其定义为一个有限域,NOTE:域其实是群的一种特例,在此不深究。
Group
Group的标准定义:
我们把它实例化,针对椭圆上的点,我们可以认为他是一个有限域,因为他满足上面的特征
- Fp中只有p(p为素数)个元素0,1,2 …… p-2,p-1;
- Fp 的加法(a+b)法则是 $a+b≡c (mod p)$;即,$(a+c)÷p$的余数 和$c÷p$的余数相同。
- Fp 的乘法(a×b)法则是 $a×b≡c (mod p)$;
- Fp 的除法(a÷b)法则是 $a/b≡c (mod p)$;
- Fp 的单位元是1,零元是 0。
同时,并不是所有的椭圆曲线都适合加密。$y^2=x^3+ax+b$是一类可以用来加密的椭圆曲线,也是最为简单的一类。下面我们就把$y2=x3+ax+b$ 这条曲线定义在Fp上:选择两个满足下列条件的小于p(p为素数)的非负整数a、b
$4a^3+27b^2≠0 (mod p)$
则满足下列方程的所有点(x,y),再加上 无穷远点O∞ ,构成一条椭圆曲线。其中 x,y属于0到p-1间的整数,并将这条椭圆曲线记为Ep(a,b)。
$y^2=x^3+ax+b (mod p)$
举例
我们看一下$y^2=x^3+x+1 (mod 23)$的图像,满足这个点是所有数据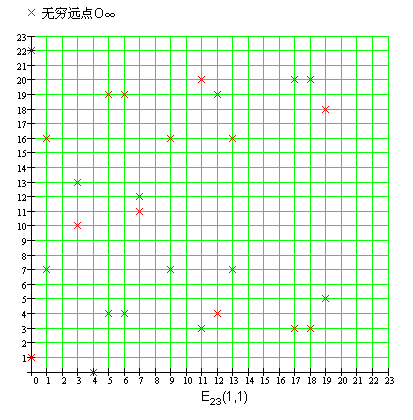
上面的结果推到公式涉及高等数学部分,我们再此就直接给出结果
- 无穷远点 O∞是零元,有O∞+ O∞= O∞,O∞+P=P
- P(x,y)的负元是 (x,-y),有P+(-P)= O∞
- P(x1,y1),Q(x2,y2)的和R(x3,y3) 有如下关系:
$$x3≡k^2-x1-x2(mod p)$$
$$y3≡k(x1-x3)-y1(mod p)$$
理想的情况下,上面的k其实就上上面直线的斜率,
$$若P=Q 则 k=(3x^2+a)/2y1$$
$$若P≠Q,则k=(y2-y1)/(x2-x1)$$
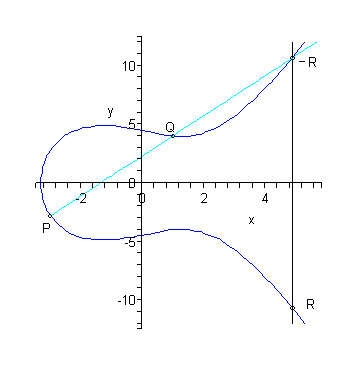
例5.1 已知E23(1,1)上两点P(3,10),Q(9,7),求1)-P,2)P+Q,3) 2P。
1) –P的值为(3,-10)
2) k=(7-10)/(9-3)=-1/2,2的乘法逆元为12 因为212≡1 (mod 23)
k≡-112 (mod 23) 故 k=11。
x=112-3-9=109≡17 (mod 23);
y=11[3-(-6)]-10=89≡20 (mod 23)
故P+Q的坐标为(17,20)
3) k=[3(32)+1]/(2*10)=1/4≡6 (mod 23)
x=62-3-3=30≡20 (mod 23)
y=6(3-7)-10=-34≡12 (mod 23)
故2P的坐标为(7,12)
在上面这个例子中如果已经知道2P = (7,12)和P(3,10),Q(9,7),你很难计算出2这个参数.
总结
本文深入介绍了椭圆曲线加密算法。
声明
本文50%为翻译组合,50%为原创
d3d3LmVoY29vLmNvbSwg5L2c6ICFOmVoY29v(BASE64编码)
引用
http://8btc.com/article-138-1.html
http://8btc.com/article-140-1.html
https://arstechnica.com/security/2013/10/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/
